LDA - Unlocking Data's Hidden Themes With Agile Precision
In the vast, ever-expanding ocean of digital information, making sense of unstructured text data can feel like an insurmountable challenge. From scientific papers to customer reviews, identifying underlying patterns and themes is crucial for insights and decision-making. This is where Latent Dirichlet Allocation, or LDA, emerges as a powerful statistical model, acting with the agility and precision of a puma in the wild, swiftly dissecting complex datasets to reveal their hidden structures.
LDA is not just another algorithm; it's a cornerstone in the field of topic modeling, offering a robust framework for understanding the abstract "topics" that permeate a collection of documents. It empowers analysts, researchers, and businesses to transform chaotic textual data into organized, interpretable knowledge. This article delves deep into the mechanics, applications, and nuances of LDA, exploring why it remains an indispensable tool for anyone looking to unlock the true potential of their textual information.
Table of Contents
- What is Latent Dirichlet Allocation (LDA)?
- The Core Mechanics of LDA: Probability and Bayesian Inference
- Navigating the Labyrinth: Determining the Optimal Number of Topics
- LDA in Action: A Professional's Perspective
- LDA vs. Word2Vec: Distinct Tools for Distinct Purposes
- LDA: An Approximation Method, Not a Single Functional (A Different Context)
- The Agility of LDA: Why It's Like a Puma in Data Analysis
- Conclusion
What is Latent Dirichlet Allocation (LDA)?
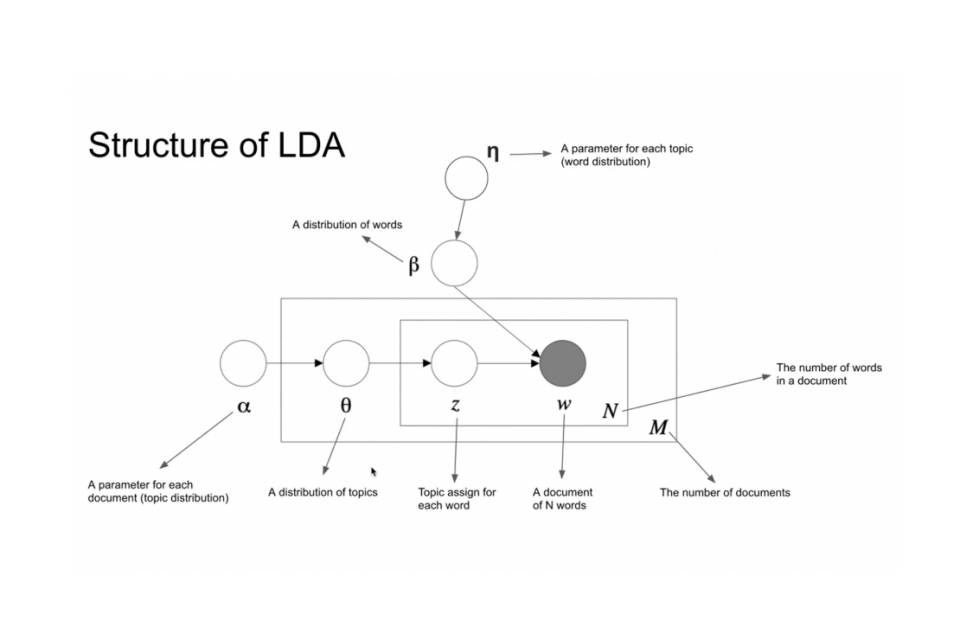
At its heart, Latent Dirichlet Allocation (LDA) is a generative statistical model designed to discover the abstract "topics" that are present in a collection of documents. Imagine having thousands of news articles, research papers, or customer reviews. Manually reading through them to identify recurring themes would be an impossible task. LDA automates this process, providing a probabilistic framework to infer these hidden structures. It operates on the principle that each document is a mixture of various topics, and each topic is a mixture of various words.
The primary goal of LDA is to classify text within documents into these specific topics. Unlike traditional hard clustering methods where a document belongs exclusively to one cluster, LDA performs what is known as "soft clustering." This means that a single document can be assigned a probability distribution over multiple topics. For instance, a document about "sustainable energy" might have a high probability of belonging to both a "renewable energy" topic and an "environmental policy" topic. This nuanced approach provides a richer, more realistic representation of document content, acknowledging the inherent complexity and multi-faceted nature of human language.
The elegance of LDA lies in its ability to uncover these latent (hidden) topics without any prior knowledge of what those topics might be. It learns them directly from the statistical relationships between words within and across documents. This unsupervised learning capability makes LDA an incredibly versatile tool for exploratory data analysis, content recommendation systems, sentiment analysis, and even forensic linguistics, providing a robust foundation for understanding large text corpora.
The Core Mechanics of LDA: Probability and Bayesian Inference
Understanding how LDA operates requires a glimpse into its probabilistic underpinnings. At its core, LDA leverages Bayesian rules to determine the posterior probability that an observed sample (a document or a word within it) belongs to a particular class (a topic). It’s a sophisticated statistical inference process that estimates the underlying topic structure based on observed word patterns.
The model assumes a generative process for documents: first, a document picks a distribution of topics; then, for each word in the document, it picks a topic from that distribution and then picks a word from the chosen topic's word distribution. The "latent" part of Latent Dirichlet Allocation refers to these hidden topic distributions and word distributions for each topic, which the algorithm aims to discover.
The complexity of LDA's parameter space is significant. The effective number of LDA parameters can be expressed as k**p + (k-1), where 'k' represents the number of topics and 'p' represents the number of words in the vocabulary. This highlights the model's capacity to capture intricate relationships within the data, making it a powerful tool for complex textual analysis. In essence, LDA provides a concise summary of the data by reducing the dimensionality of the document-word matrix into a more interpretable document-topic and topic-word matrix. This abstraction allows for a high-level understanding of vast datasets.
LDA's Generalization: Beyond pLSA
One of the key insights into LDA's design is its relationship to its predecessor, Probabilistic Latent Semantic Analysis (pLSA). From a mathematical perspective, LDA is considered a generalization of pLSA. This means that under specific conditions, particularly when LDA's hyperparameters are set to certain values, it can specialize into the pLSA model. This architectural elegance allows LDA to offer greater flexibility and robustness in practical applications.
The primary advantage of LDA over pLSA lies in its use of Dirichlet priors. These priors act as smoothing factors, preventing overfitting and enabling LDA to handle unseen documents more effectively. While pLSA learns topic distributions directly from the training data, which can lead to issues with new documents, LDA assumes that topic distributions are drawn from a Dirichlet distribution. This Bayesian approach provides a more robust and generalized model, making LDA a more reliable choice for real-world topic modeling tasks and enhancing its "puma-like" adaptability across diverse datasets.
Navigating the Labyrinth: Determining the Optimal Number of Topics
A critical challenge in applying LDA, and indeed any topic model, is determining the optimal number of topics (k). This isn't a trivial decision, as too few topics might over-generalize, while too many might create overly specific or redundant themes. Fortunately, researchers have developed several metrics and visualization techniques to guide this process, allowing for precise calibration of the LDA - pumas model.
According to previous papers on LDA, perplexity, coherence, and bubble charts are all valid methods for determining the appropriate number of topics. Perplexity measures how well a probability model predicts a sample. A lower perplexity generally indicates a better model. However, it's crucial not to rely solely on the perplexity curve. Sometimes, the perplexity curve might not show a clear "elbow" or optimal point, leading practitioners to believe the classification is ineffective.
This is where coherence scores and visual tools like bubble charts become invaluable. Coherence measures the semantic similarity between the high-scoring words in a topic. A higher coherence score suggests that the words within a topic are semantically related and thus form a meaningful theme. Bubble charts, on the other hand, provide a visual representation of topic relationships and word distributions, allowing human judgment to play a role in assessing the quality and distinctiveness of the topics. By combining these quantitative and qualitative measures, one can confidently identify the number of topics that best represents the underlying structure of the data.
Perplexity-Var: A Metric for Model Efficacy
Further refining the evaluation of LDA models, the Perplexity-Var indicator offers a dual perspective on model performance. Firstly, it considers the model's generalization ability. A smaller Perplexity value indicates that the LDA model has better generalization capability, meaning it can more accurately predict unseen data. This is crucial for real-world applications where the model needs to perform well on new, incoming documents.
Secondly, Perplexity-Var also sheds light on the effectiveness of LDA's topic extraction. When the average similarity of the topic structure is minimized, it corresponds to an LDA model that is effectively extracting distinct and well-defined topics. This metric helps to ensure that the topics identified are not only statistically sound but also semantically meaningful and distinct from one another. By optimizing for both low perplexity and minimal topic similarity, practitioners can fine-tune their LDA models to achieve superior performance in both predictive accuracy and thematic clarity.
LDA in Action: A Professional's Perspective
From a practical standpoint, the LDA topic model is particularly well-suited for processing long texts. Unlike methods that might struggle with extensive documents, LDA excels at dissecting detailed articles, reports, or literary works, uncovering their multifaceted thematic compositions. This makes it an invaluable tool for researchers, content strategists, and data scientists dealing with large volumes of rich, descriptive text.
As pointed out in previous discussions, the LDA topic model effectively performs document clustering. However, it's not a rigid, "hard clustering" where each document belongs to only one group. Instead, it's a "soft clustering" process. This means that a document can belong to multiple topics simultaneously, albeit with varying degrees of probability. For instance, a lengthy research paper on "artificial intelligence in healthcare" might be strongly associated with topics like "machine learning algorithms," "medical diagnostics," and "ethical considerations in AI." This soft assignment provides a more nuanced and realistic representation of complex documents, reflecting the interdisciplinary nature of many real-world texts.
This soft clustering capability, combined with its ability to handle long texts, positions LDA as a professional-grade solution for various applications. It can be used for automated content tagging, improving search relevance, categorizing customer feedback, or even analyzing historical documents to trace the evolution of ideas. The agility of LDA in handling these diverse and often challenging datasets truly showcases its power, much like a puma adapting to varied terrains.
The Spectrum of LDA Models: Beyond the Basics
While Latent Dirichlet Allocation (LDA) serves as the foundational model for topic discovery, the field has evolved to include a rich spectrum of extensions and variations, each designed to address specific analytical needs or incorporate additional information. These advanced models build upon LDA's core principles, offering enhanced capabilities for more complex data scenarios. Understanding this diversity is key to leveraging the full power of LDA - pumas for nuanced text analysis.
Some notable models in this expanded family include:
- Labeled LDA (LLDA Model): This variant incorporates document labels (e.g., categories or tags) into the topic modeling process, allowing the model to learn topics that are consistent with pre-defined categories.
- Partially Labeled LDA (PLDA Model): Building on LLDA, PLDA is designed for situations where only a subset of documents has labels, making it highly practical for real-world datasets with incomplete annotations.
- Supervised LDA (SLDA Model): SLDA extends LDA to predict an observed response variable (e.g., sentiment score, star rating) associated with each document, making it useful for tasks like predicting outcomes based on text content.
- Dirichlet Multinomial Regression (DMR Model): This model allows covariates (e.g., author, publication year) to influence the topic proportions within documents, providing a way to analyze how external factors shape thematic content.
- Generalized Dirichlet Multinomial Regression (GDMR Model): An extension of DMR, offering even greater flexibility in modeling the relationship between covariates and topic distributions.
- Hierarchical Dirichlet Process (HDP Model): A non-parametric Bayesian model that automatically infers the number of topics from the data, removing the need for pre-specifying 'k', which is a significant advantage in exploratory analysis.
This array of models demonstrates the adaptability and continuous development within the LDA framework, allowing practitioners to select the most appropriate tool for their specific data and research questions, further cementing LDA's role as a versatile and powerful analytical paradigm.
LDA vs. Word2Vec: Distinct Tools for Distinct Purposes
In the rapidly evolving landscape of natural language processing (NLP), it's common for newcomers to sometimes conflate different techniques. A frequent point of confusion arises when comparing Latent Dirichlet Allocation (LDA) with Word2Vec. It's crucial to understand that from a model perspective, LDA and Word2Vec have almost no significant connection. They serve fundamentally different purposes and operate on different principles, even though both deal with textual data.
Word2Vec is a method for generating "word embeddings," which are vector representations of words. The core idea is that words that appear in similar contexts will have similar vector representations. These word vectors capture semantic relationships between words, allowing for tasks like identifying synonyms, analogies, or understanding word similarity. Word2Vec is a tool for representing individual words in a numerical space.
On the other hand, LDA is a topic model. Its primary function is to analyze a collection of documents (a "corpus") and identify the underlying abstract topics present within them. As noted in the provided data, one of LDA's roles is to process the document-word matrix. It transforms this matrix into a document-topic matrix and a topic-word matrix, essentially revealing what topics are in each document and what words define each topic. It does not create word embeddings in the same way Word2Vec does.
While both contribute to understanding text, their focus differs. Word2Vec helps understand individual words and their relationships, while LDA helps understand documents and their thematic content. They are complementary rather than competing technologies. One might even use word embeddings generated by Word2Vec as features for other models, or analyze the words within LDA-generated topics using word embeddings to gain deeper semantic insights. But as models themselves, they are distinct, each with its unique strengths and applications in the broader field of NLP, much like a puma and a cheetah are both agile cats but adapted for different hunting strategies.
LDA: An Approximation Method, Not a Single Functional (A Different Context)
It's important to acknowledge that the acronym "LDA" appears in different scientific domains, referring to distinct concepts. While our primary focus in this article is Latent Dirichlet Allocation for topic modeling, the provided "Data Kalimat" also briefly touches upon LDA in the context of Density Functional Theory (DFT). This highlights a common challenge in interdisciplinary discussions: identical acronyms can signify entirely different concepts.
In the realm of quantum chemistry and condensed matter physics, LDA stands for "Local Density Approximation." This LDA is described as the simplest exchange-correlation functional and was proposed very early on, almost concurrently with DFT itself. Crucially, the "Data Kalimat" clarifies that LDA (in this context) is not the name of a single functional but rather an approximation method that encompasses many functionals. It's a foundational concept in calculating the electronic structure of materials.
This distinction is vital. The LDA for topic modeling is a statistical model for text analysis, while the LDA in DFT is a quantum mechanical approximation for electron interactions. They share an acronym but operate on completely different principles and are applied to vastly different problems. This serves as a reminder to always consider the context when encountering acronyms, ensuring clarity and avoiding confusion between disparate scientific fields. Our discussion of "lda - pumas" remains firmly rooted in the topic modeling context, where LDA's agility in data analysis is paramount.
The Agility of LDA: Why It's Like a Puma in Data Analysis
The metaphor of a "puma" perfectly encapsulates the essence of Latent Dirichlet Allocation (LDA) in the world of data analysis. Pumas are known for their stealth, power, and incredible agility – traits that mirror LDA's capabilities in dissecting complex textual datasets. Just as a puma can silently track its prey through dense foliage, LDA can subtly uncover hidden patterns and themes within vast, unstructured text corpora.
Consider the power of LDA. It can ingest millions of documents, each potentially thousands of words long, and probabilistically infer the underlying topics without any human intervention. This is akin to a puma's raw strength, capable of bringing down targets far larger than itself. The ability to perform "soft clustering" means LDA doesn't force documents into rigid categories but acknowledges their multi-faceted nature, assigning them probabilities across various themes. This flexibility is a hallmark of its power, allowing for a more nuanced and realistic understanding of information.
The agility of LDA is evident in its adaptability. Whether dealing with short social media posts or extensive academic journals, LDA can be configured and refined (through metrics like perplexity and coherence) to extract meaningful insights. Its various extensions, such as LLDA, SLDA, and HDP, further enhance its adaptability, allowing it to incorporate labels, predict outcomes, or even determine the number of topics automatically. This chameleon-like ability to adjust to different data characteristics and analytical goals makes LDA an exceptionally versatile tool, always ready to pounce on new data challenges.
Moreover, the precision of LDA, particularly when guided by metrics like Perplexity-Var, ensures that the topics extracted are not just statistically significant but also semantically coherent and distinct. This precision is vital for deriving actionable insights, much like a puma's precise strike. In an era where information overload is the norm, the ability of LDA to efficiently and accurately distill vast amounts of text into coherent, interpretable themes makes it an indispensable asset. It empowers us to navigate the data jungle with the confidence and effectiveness of a true predator, revealing the hidden structures that drive understanding and innovation.
Conclusion
Latent Dirichlet Allocation (LDA) stands as a testament to the power of statistical modeling in transforming raw, unstructured text into meaningful, actionable insights. From its core probabilistic mechanics and Bayesian inference to its sophisticated methods for determining optimal topic numbers, LDA offers a robust and flexible framework for understanding the hidden thematic structures within vast document collections. Its ability to perform "soft clustering" and its continuous evolution into specialized models like LLDA and HDP underscore its adaptability and enduring relevance in the ever-growing field of natural language processing.
As we've explored, LDA's capacity to dissect complex textual data with precision and efficiency truly embodies the metaphor of a "puma" – agile, powerful, and exceptionally adept at uncovering hidden patterns. While distinct from other NLP tools like Word2Vec and from the LDA found in Density Functional Theory, Latent Dirichlet Allocation for topic modeling carves out its own indispensable niche. It empowers researchers, analysts, and businesses to move beyond surface-level understanding, enabling deeper dives into the contextual meaning and thematic organization of information.
In a world increasingly driven by data, the ability to effectively analyze and interpret textual information is paramount. LDA provides a proven, powerful means to achieve this, making the seemingly impossible task of understanding massive datasets not only feasible but also remarkably insightful. We encourage you to delve deeper into the fascinating world of topic modeling and discover how LDA can unlock the hidden potential within your own data. What hidden themes are waiting to be uncovered in your documents? Share your thoughts and experiences with LDA in the comments below, or explore our other articles on advanced data analysis techniques to further sharpen your analytical prowess!

Latent Dirichlet Allocation (LDA)
Lda
Linear Discriminant Analysis